GPS and Tectonics

GPS aids us in better understanding our planet by allowing us to measure how the surface of the Earth moves. Much of this motion causes earthquakes, builds mountains, and, indirectly, creates volcanoes.

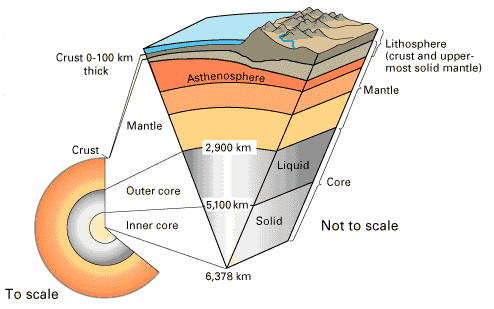
The surface of the Earth is broken up into "tectonic plates" that move in different directions and speeds (Figure 1). The plates are made of the lithosphere, a layer consisting of the crust and the uppermost, solid part of the mantle (Figure 2). The plates move rigidly, each as one solid piece. They ride on the layer underneath the lithosphere, called the asthenosphere, which is hotter - and bends rather than breaks.

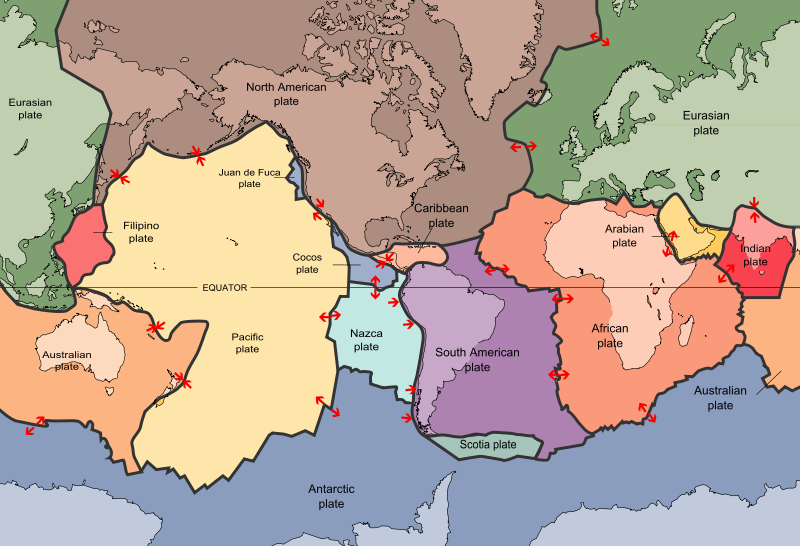
Figure 1.The Earth's surface is comprised of tectonic plates, which move independently of each other. The sense of motion between the plates is shown by the red arrows (Credit: USGS.)

Figure 2.The internal structure of Earth. Tectonic plates are made of the lithosphere, a layer consisting of the crust and the upper, rigid layer of the mantle. The lithosphere rides on the asthenosphere, a hotter layer that oozes rather than breaks. (Credit: USGS.)

To study present-day plate motions, we can anchor GPS instruments firmly in bedrock and measure how they move along with the tectonic plate. Each arrow in Figure 3 shows the predicted motions of locations on Earth. The longer the arrow, the faster the site is moving. Plate boundaries are shown in white. In Figure 4 we see the observed motions as measured by GPS. Do they roughly agree?

ectonic plates are on a globe, not on a flat surface. Each plate rotates about a "pole" and each plate also has a different speed. The farther you are from the pole of rotation, the bigger the speed of your GPS station. By observing tectonic motion with GPS instruments, we can learn what is pushing and pulling at the Earth's surface—and what happens when it does.

Classroom exercise: Visualizing Relationships with Data: Exploring plate boundaries with Earthquakes, Volcanoes, and GPS Data | Western U.S. and Alaska

Figure 3.A map of the velocities predicted for a plate motion model. Plate boundaries are shown in white. (Credit: Pearson Prentice Hall.)

Figure 4.Measured motion of GPS sites. Plate boundaries are shown in green. (Credit: Zuheir Altamimi, ITRF.)

Rigid Body Motion

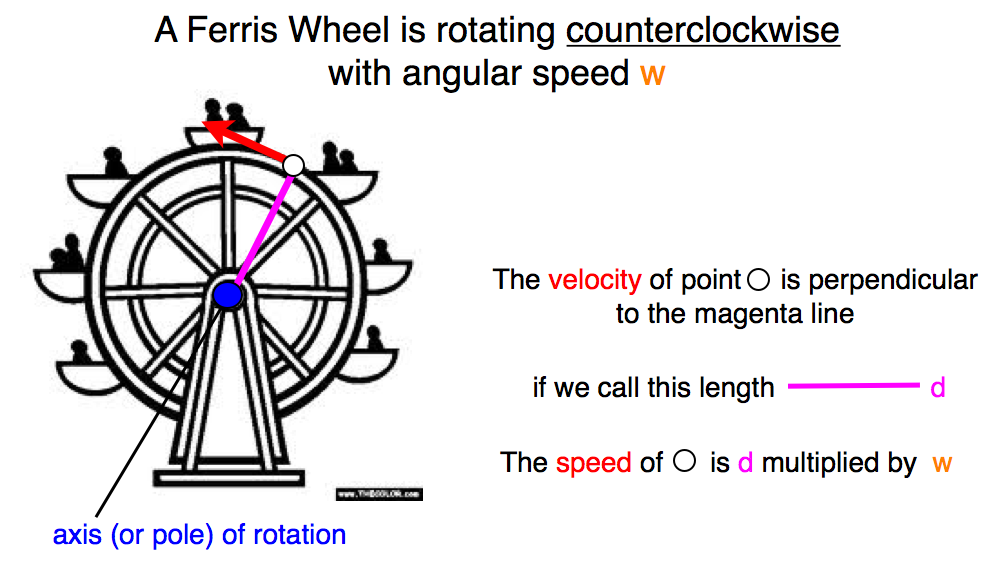
It is a little complicated to calculate the motion of a tectonic plate. But you can understand the motion of a tectonic plate if you think about a simple two-dimensional case. In Figure 5 we have a Ferris wheel. It is rotating counterclockwise. How fast it rotates is called its angular speed. The wheel rotates about the center point. This is called the "pole of rotation" or "axis" of rotation." The speed of any point on the Ferris wheel can be calculated by multiplying the distance between the pole of rotation and the point (d) and the angular speed (w).

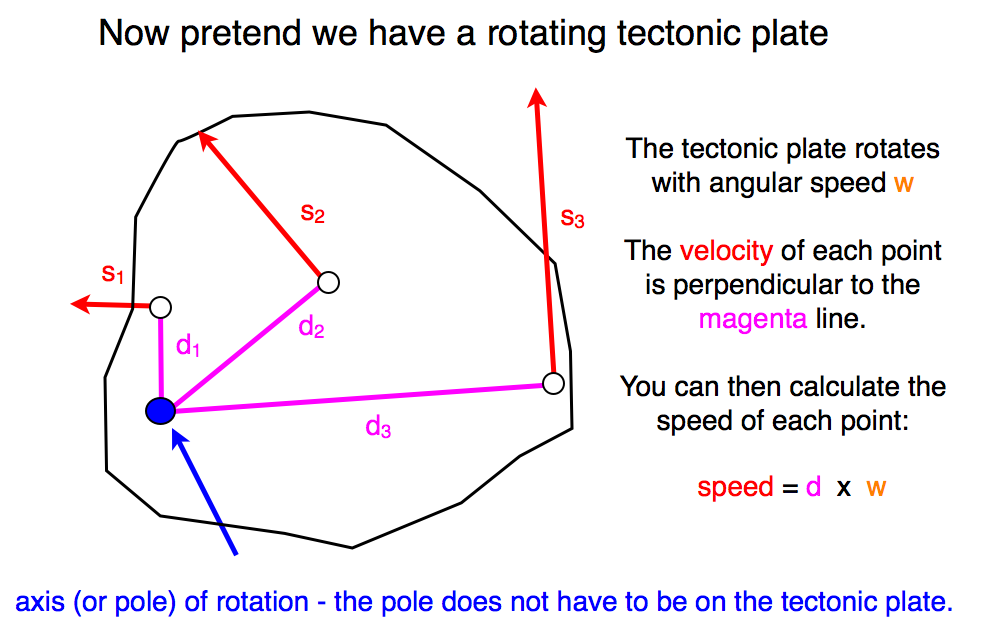
You can think of a tectonic plate the same way (Figure 6). The speed of any point on the plate is the product of the angular speed w and the distance between the rotation pole and the point d. You can figure out the direction of speed (meaning the velocity) because it is perpendicular to d. This means that GPS stations on a tectonic plate are moving faster the farther away they are from the axis of rotation.

A final thing to point out - all the motion takes place in this two-dimensional space, which means there is no vertical motion. This is also true for real plate tectonics. This means that if the GPS station is on the rigid part of the tectonic plate, there should be not vertical motion. If there is vertical motion, that means something else is going on.

Figure 5.Example of rigid body motion using a Ferris Wheel. The speed of any point is the multiplication of the angular speed and the distance between the point and the axis of rotation. Credit: Kristine Larson.

Figure 6.Example of rigid body motion for a two-dimensional tectonic plate. The same rules are used here as were used for the Ferris wheel. The main difference is that a Ferris Wheel rotates pretty quickly but a tectonic plate only rotates several degrees every million years. Credit: Kristine Larson.

GPS and Tectonics

The Earth's surface is comprised of tectonic plates, which move independently of each other. The sense of motion between the plates is shown by the red arrows (Credit: USGS.)

The internal structure of Earth. Tectonic plates are made of the lithosphere, a layer consisting of the crust and the upper, rigid layer of the mantle. The lithosphere rides on the asthenosphere, a hotter layer that oozes rather than breaks. (Credit: USGS.)

A map of the velocities predicted for a plate motion model. Plate boundaries are shown in white. (Credit: Pearson Prentice Hall.)

Measured motion of GPS sites. Plate boundaries are shown in green. (Credit: Zuheir Altamimi, ITRF.)

Rigid Body Motion

Figure 5.Example of rigid body motion using a Ferris Wheel. The speed of any point is the multiplication of the angular speed and the distance between the point and the axis of rotation. Credit: Kristine Larson.

Example of rigid body motion for a two-dimensional tectonic plate. The same rules are used here as were used for the Ferris wheel. The main difference is that a Ferris Wheel rotates pretty quickly but a tectonic plate only rotates several degrees every million years. Credit: Kristine Larson.

Funding and Acknowledgements